EECS-498

Posted on In

lecture 2: Image Classification

Nearest Neighbor

L1(Manhattan) distance

$d{1}(I{1},I{2})=\sum{p}|I{1}^{p},I{2}^{p}|$

complexity: training:O(1）；testing:O(n)

L2(Euclidean) distance

$d{2}(I{1},I{2})=\sqrt{\sum{p}(I{1}^{p},I{2}^{p})^2}$

Assignment 1

Tensor Basics

Creating and Accessing tensors

A torch tensor is a multidimensional grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the tensor; the shape of a tensor is a tuple of integers giving the size of the array along each dimension.

We can initialize torch tensor from nested Python lists. We can access or mutate elements of a PyTorch tensor using square brackets.

Accessing an element from a PyTorch tensor returns a PyTorch scalar; we can convert this to a Python scalar using the .item() method

Tensor constructors

PyTorch provides many convenience methods for constructing tensors; this avoids the need to use Python lists, which can be inefficient when manipulating large amounts of data. Some of the most commonly used tensor constructors are:

Datatypes

Each tensor has a dtype attribute that you can use to check its data type

We can cast a tensor to another datatype using the .to() method; there are also convenience methods like .float() and .long() that cast to particular datatypes

PyTorch provides several ways to create a tensor with the same datatype as another tensor:

  • PyTorch provides tensor constructors such as torch.zeros_like() that create new tensors with the same shape and type as a given tensor
  • Tensor objects have instance methods such as .new_zeros() that create tensors the same type but possibly different shapes
  • The tensor instance method .to() can take a tensor as an argument, in which case it casts to the datatype of the argument

Tensor indexing

Slice indexing

similar to python

There are two common ways to access a single row or column of a tensor: using an integer will reduce the rank by one, and using a length-one slice will keep the same rank.

you can use the clone() method to make a copy of a tensor

Integer tensor indexing

We can also use index arrays to index tensors

More generally, given index arrays idx0 and idx1 with N elements each, a[idx0, idx1] is equivalent to:

1
2
3
4
5
6
torch.tensor([
  a[idx0[0], idx1[0]],
  a[idx0[1], idx1[1]],
  ...,
  a[idx0[N - 1], idx1[N - 1]]
])

Boolean tensor indexing

Boolean tensor indexing lets you pick out arbitrary elements of a tensor according to a boolean mask. Frequently this type of indexing is used to select or modify the elements of a tensor that satisfy some condition.

In PyTorch, we use tensors of dtype torch.bool to hold boolean masks

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Find the elements of a that are bigger than 3. The mask has the same shape as
# a, where each element of mask tells whether the corresponding element of a
# is greater than three.
mask = (a > 3)
print('\nMask tensor:')
print(mask)

# We can use the mask to construct a rank-1 tensor containing the elements of a
# that are selected by the mask
print('\nSelecting elements with the mask:')
print(a[mask])

# We can also use boolean masks to modify tensors; for example this sets all
# elements <= 3 to zero:
a[a <= 3] = 0
print('\nAfter modifying with a mask:')
print(a)

Reshaping operations

View

PyTorch provides many ways to manipulate the shapes of tensors. The simplest example is .view(): This returns a new tensor with the same number of elements as its input, but with a different shape.

We can use .view() to flatten matrices into vectors, and to convert rank-1 vectors into rank-2 row or column matrices

As a convenience, calls to .view() may include a single -1 argument; this puts enough elements on that dimension so that the output has the same number of elements as the input.

shares the same data!

Swapping axes

The simplest such function is .t(), specificially for transposing matrices

For tensors with more than two dimensions, we can use the function torch.transpose) to swap arbitrary dimensions.

If you want to swap multiple axes at the same time, you can use torch.permute) method to arbitrarily permute dimensions

Contiguous tensors

you can typically overcome these sorts of errors by either by calling .contiguous() before .view(), or by using .reshape() instead of .view()

Tensor operations

Elementwise operations

Basic mathematical functions operate elementwise on tensors, and are available as operator overloads, as functions in the torch module, and as instance methods on torch objects

Reduction operations

We may sometimes want to perform operations that aggregate over part or all of a tensor, such as a summation; these are called reduction operations.

Like the elementwise operations above, most reduction operations are available both as functions in the torch module and as instance methods on tensor objects.

We can use the .sum() method (or eqivalently torch.sum) to reduce either an entire tensor, or to reduce along only one dimension of the tensor using the dim argument.Other useful reduction operations include mean, min, and max

After summing with dim=d, the dimension at index d of the input is eliminated from the shape of the output tensor

Reduction operations reduce the rank of tensors: the dimension over which you perform the reduction will be removed from the shape of the output. If you pass keepdim=True to a reduction operation, the specified dimension will not be removed; the output tensor will instead have a shape of 1 in that dimension

torch.argmin:This is the second value returned by torch.min()

Matrix operations

  • torch.dot: Computes inner product of vectors
  • torch.mm: Computes matrix-matrix products
  • torch.mv: Computes matrix-vector products
  • torch.addmm / torch.addmv: Computes matrix-matrix and matrix-vector multiplications plus a bias
  • torch.bmm / torch.baddmm: Batched versions of torch.mm and torch.addmm, respectively
  • torch.matmul: General matrix product that performs different operations depending on the rank of the inputs. Confusingly, this is similar to np.dot in numpy
  • torch.stack(tensors, dim=0, **, out=None*) :Concatenates a sequence of tensors along a new dimension

Vectorization

avoiding explicit Python loops in your code and instead using PyTorch operators to handle looping internally will cause your code to run a lot faster. This style of writing code, called vectorization, avoids overhead from the Python interpreter, and can also better parallelize the computation (e.g. across CPU cores, on on GPUs)

Broadcasting

Broadcasting usually happens implicitly inside many PyTorch operators. However we can also broadcast explicitly using the function torch.broadcast_tensors

torch.mm does not support broadcasting, but torch.matmul does

Out-of-place vs in-place operators

Out-of-place operators: return a new tensor

In-place operators: modify and return the input tensor

Running on GPU

ll PyTorch tensors also have a device attribute that specifies the device where the tensor is stored — either CPU, or CUDA (for NVIDA GPUs)

we can use the .to() method to change the device of a tensor. We can also use the convenience methods .cuda() and .cpu() methods to move tensors between CPU and GPU

Calling x.to(y) where y is a tensor will return a copy of x with the same device and dtype as y

Other

torch.topk(input, k, dim=None, largest=True, sorted=True, **, out=None*):Returns the k largest elements of the given input tensor along a given dimension

torch.chunk(input, chunks, dim=0)：split tensor tuple

torch.cat(tensors, dim=0, **, out=None*):torch.cat() can be seen as an inverse operation for torch.split() and torch.chunk()

lecture 3:Linear Classifier

different viewpoint

Algebraic Viewpint

Visual VIewpoint

图片

Geometric Viewpoint

图片

Multiclass SVM Loss(hinge loss)

The score of the correct class should be higer than all the other scores

图片

score:s=f(xi,W)

$Li=\sum{j\ne yi}max(0,s{j}-s_{y_i}+1)$

Regularization

$L(W)=1/N\sum_{i=1}^NL_i(f(x_i,W),y_i)+\lambda R(W)$

$\lambda R(W)$:Regularization:Prevent the model from doing too well on traing data

simple examples:

L2 regularization:$R(W)=\sumk\sum_lW{k,l}^2$

L1 regularization:$R(W)=\sumk\sum_l|W{k,l}|$

L2 regularization:$R(W)=\sumk\sum_l\beta W{k,l}^2+|W_{k,l}|$

goal:1.express preferences;2.avoid overfitting;.improve optimization by adding curvature

图片

Cross-Entropy Loss(Multinomial Logistic Regression)

comapre the m pv):maximum likelihood estimation

lecture 4:Optimization

$w^*=argmin_wL(w)$

SGD+Momentum

Build up “velocity” as a running mean of gradients

$\rho$ gives “friction”;typically rho=0.9 or 0.99

$v_{t+1}=\rho v_t+\nabla f(x_t)$

$x{t+1}=x_t-\alpha v{t+1}$

1).At local minimum we still have some velocity that can help escape

2).smooth out the noise ,alleviate oscillatory problem

Nesterov Momentum

图片

“Look ahead” to the point where updating using velocity would take us; compute gradient there and mix it with velocity to get actual update direction

$v_{t+1}=\rho v_t-\alpha\nabla f(x_t+\rho v_t)$

$x{t+1}=x_t+v{t+1}$

AdaGrad

1
2
3
4
5
grad_squared=0
for t in range(num_steps):
    dw=compute_gradient(w)
    grad_squared+=dw*dw
    w-=learning_rate*dw/(grad_quared.sqrt()+1e-7)

progress along “steep”directions is damped

progress along “flat”directions is accelerated

RMSProp:”Leak Adagrad”

1
2
3
4
5
grad_squared=0
for t in range(num_steps):
    dw=compute_gradient(w)
    grad_squared+=decay_rate*grad_squared+(1-decay_rate)*dw*dw
    w-=learning_rate*dw/(grad_quared.sqrt()+1e-7)

avoid slowing down when square becomes bigger

Adam: RMSProp+Momentum

1
2
3
4
5
6
7
moment1=0
moment2=0
for t in range(num_steps):
    dw=compute_gradient(w)
    moment1=beta1*moment1+(1-beta1)*dw #similar to velocity
    moment2=beta2*moment2+(1-beta2)*dw*dw
    w-=learning_rate*moment1/(moment2.sqrt()+1e-7)

Bias correction for the fact that the first and the second moment estimates start at zero

1
2
3
4
5
6
7
8
9
moment1=0
moment2=0
for t in range(num_steps):
    dw=compute_gradient(w)
    moment1=beta1*moment1+(1-beta1)*dw #similar to velocity
    moment2=beta2*moment2+(1-beta2)*dw*dw
    moment1_unbias=moment1/(1-beta1**t)
    moment2_unbias=moment2/(1-beta2**t)
    w-=learning_rate*moment1_unbias/(moment2_unbias.sqrt()+1e-7)

图片

lecture 5:Neural Networks

Feature transforms

Fully-connected neural network:also MLP

Lecture 6:Back Propagation

Represent complex expressions as computational graphs

During the backward pass, each node in the graph receives upstream gradients and multiplies them by local gradients to compute downstream gradients

Backprop can be implemented with “flat” code where the backward pass looks like forward pass reversed

Lecture 7：Convolutional Networks

Receptive Fields

Each successive convolution adds K-1 to the receptive field size

With L layers the receptive field size is 1+L*(K-1)

图片

Strided Convolution

a way to add receptive field size quickly

LeNet

spatial size decreases:using pooling or strived conv

number of channels increases:total “volume” is preserved

Lecture 8：CNN Architecture

ZFNet:a bigger AlexNet

VGG

5x5=2 layer of 3x3 in receptive fields,but less FLOPS and fewer parametres;and it can add more relu between layers

ResNet

Bottleneck Block:More layers, less computational cost

图片

ResNeXt

图片

add groups improves performance with same computational complexity

Squeeze-and-Excitation Networks

图片

Densely Connected Neural Networks

图片

Dense blocks where each layer is connected to every other layer in feedforward fashion

Alleviates vanishing gradient,strengthens feature propagation,encourages feature reuse

MobileNets:Tiny Networks(For MObile Devices)

图片

Lecture 9: Hardware and Software

autograd

requires_grad=True

Static Computation Graphs

graph=build_graph()

reuse the same graph on every iteration

graph=torch.jit.script(model):

Just-In-Time compilation:introspect the source code of the function,compile it into a graph object

advantage:optimization;serialize

diadvantage:debug

Lecture 10: Training Neural Networks I

One time setup

Activation functions, data preprocessing, weight initialization, regularization

Activation functions

Leaky ReLU

f(x)=max(0.01x,x):will not die

PReLU(parametric)

$f(x)=max(\alpha x,x) where\ \alpha\ is\ learnable$

Exponential Linear Unit(ELU)

$f(x)=x\ if\ x>0$

$f(x)=\alpha (exp(x)-1)\ if\ x>0$

closer to zero mean outputs

negative saturation regime compared with Leaky ReLU adds some robustness to noise

Scaled Exponential Linear Unit(SELU)

$f(x)=\lambda x\ if\ x>0$

$f(x)=\lambda\alpha (exp(x)-1)\ if\ x>0$

works better for deep networks

“self-normalizing”property;can train deep SELU networks without BatchNorm

Data Preprocessing

standardlize:less sensitive to small changes in weight,easier to optimize

图片

Weight Initialization

Gaussion:not good for deep network

Xavier Initialization

w=np.random.randn(Din,Dout)/np.sqrt(Din)

variance of output=variance of input->std:1/sqrt(Din)

problem:change from tanh to ReLU,activations collapse to zero again because Xavier assumes zero centred activation function

Kaiming/MSRA Initialization

std=sqrt(2/Din)

problem: not good for ResNet->intialize first conv with MSRA,second to zero

Regularization

batch normalization and data augmentation almost always a good idea

Dropout

for large fully-connected layers

dropout makes output random->$\int p(z)f(x,z)dz$

At test time, drop nothing and multiply by dropout probability:output at test time=expected output at traing time

inverted dropout:drop and scale during traing;test time is unchanged

Others

dropconnect:drop random connections between neurons(set weight to 0)

fractional max pooling:use randomized pooling regions

stochastic depth:skip some residual blocks in ResNet

cutout:set random images regions to 0

mixup:train on random blends of image

Lecture 11: Training Neural Networks II

2.Training dynamics Learning rate schedules; hyperparameter optimization

3.After training Model ensembles, transfer learning

Learning Rate Schedule

Learing Rate Decay:Step

reduce learning rate at a few fixed points

Learing Rate Decay:Sosine

$\alpha_t=1/2\alpha_0(1+cos(t\pi/T))$

Learing Rate Decay:Linear

$\alpha_t=\alpha_0(1-t/T)$

Learing Rate Decay:Inverse Sqrt

$\alpha_t=\alpha_0/\sqrt{t}$

Choosing Hyperparameters

grid search

random search

Model Ensembles

  1. Train multiple independent models 2. At test time average their results

Transfer Learning

feature extracter;fine tuning

Lecture 12: Recurrent Networks

key idea: RNNs have an “internal state” that is updated as a sequence is processed

$ht=f_W(h{t-1},x_t)$

Vanilla/Elman RNN

$ht=tanh(W{hh}h{t-1}+W{xh}x_t)$

$y{t}=W{hy}h_{t}$

Truncated Backpropagation Through Time

only backpropagate through finite chunks of the sequence

Example： Image Captioning

图片

Long Short Term Memory(LSTM)

图片

two vectors at each timestep: cell state and hidden state

four gates

图片

i:input gate,whether to write cell

f: forget gate,whether to erase cell

o:output gate,whether to reveal cell

g:gategate,how much to write to cell

图片

Highway Networks

图片

Gated Recurrent Unit(GRU)

Lecture 13: Attention

图片

Sequence-to-Sequence with RNNs and Attention

图片

how much should we attend to each hidden state of the encoder given the current state of the decoder

图片

Attention Layer

scaled similarity function:dot product

multiple query vectors

seperate key and value

图片

Self-Attention Layer

图片

don’t know the order of the vectors->positon embedding

Y1:This produces the output of the self-attention layer at this position

Clearly the word at this position will have the highest softmax score, but sometimes it’s useful to attend to another word that is relevant to the current word.

Masked Self-Attention Layer

图片

Multihead Self-Attention Layer

1.It expands the model’s ability to focus on different positions.

2.It gives the attention layer multiple “representation subspaces”.

图片

Three Ways of Processing Sequences

图片

Transformer

图片

For RNNs, instead of only encoding the whole sentence in a hidden state, each word has a corresponding hidden state that is passed all the way to the decoding stage. Then, the hidden states are used at each step of the RNN to decode.

img

img

img

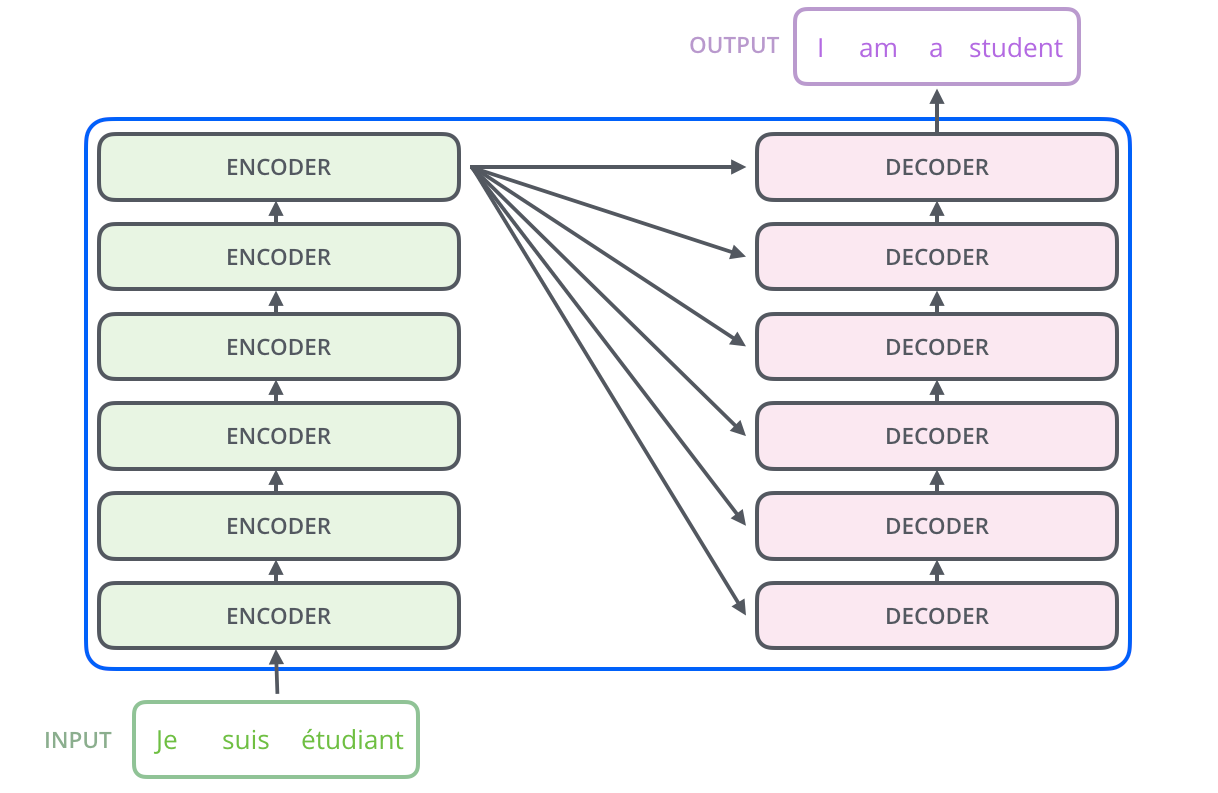
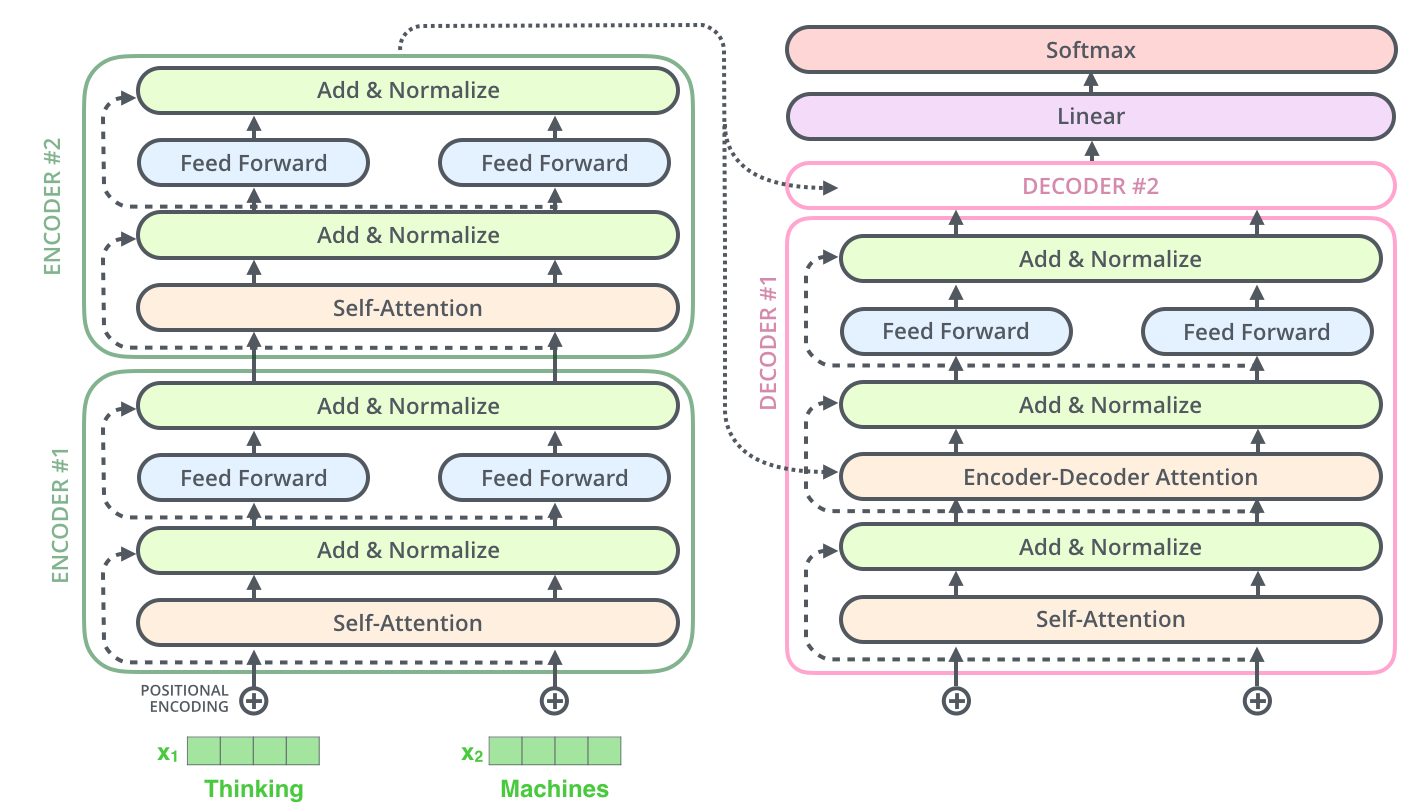
The Decoder Side

The encoder start by processing the input sequence. The output of the top encoder is then transformed into a set of attention vectors K and V. These are to be used by each decoder in its “encoder-decoder attention” layer which helps the decoder focus on appropriate places in the input sequence

图片

img

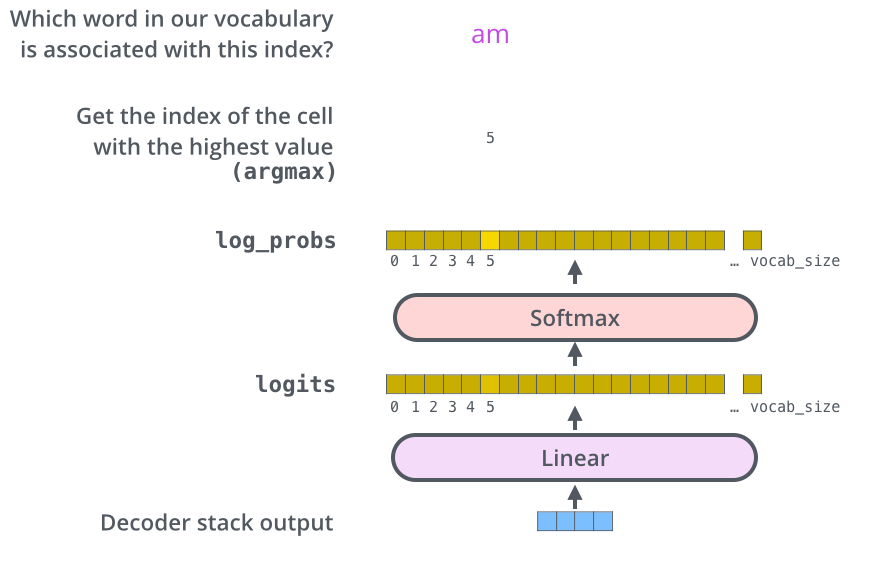
Lecture 14: Visualizing and Understanding

Lecture 19: Generative Models I

Discriminative Model: learn a probability distribution p(y|x)

Generative Model: learn a probability distribution p(x)

Conditional Generative Model: learn p(x|y)

图片

Autoregressive Models

goal:write down an explicit function for p(x)=f(x,W)

given dataset $x^{(i)}$,train the model by solving$W^*=argmax\prod_ip(x^{(i)})=argmax\sum_ilogf(x^{(i)},W)$

图片

PixelRNN

generate from the upper left corner

compute a hidden state for each pixel that depends on hidden states and RGB values from the left and the above (LSTM)

$h{x,y}=f(h{x-1,y},h_{x,y-1},W)$

at each pixel,predict R,G,B:softmax over (0,1…255)

图片

slow

PixelCNN

slow

Variational Autoencoders

VAE define an intratable density that we cannot explicitly compute or optimize ,but can directly optimize a lower bound on the density

Autoencoders

图片

cmompress to low dimention

cnn;up cnn

no probabilistic: no way to sample new data from learned model

Variational Autoencoders

x is an image, z is latent factors(unobserved) used to generate x

Decoder must be probabilistic: Decoder inputs z, outputs mean μx|z and (diagonal) covariance ∑x|z ->Sample x from Gaussian with mean μx|z and (diagonal) covariance ∑x|z

After training(test)

1.sample a new latent variable from the prior distribution

2.z-decoder-x’s distribution

图片

assume simple prior p(z): Gaussian

assume the probability over the image:gaussian with a number of the gaussian equal to the numer of pixels->parametrize:mean value and standard deviation value for each pixel

output a high dimentional gaussian distribution

represent p(x|z) with a neural network

Train

maximize likelihood

图片

$p_{\theta}(x|z)$:decoder

$p_{\theta}(z)$:gaussian

Solution: Train another network (encoder) that learns $q{\phi}(z|x)=p{\theta}(z|x)$

图片

Math

图片

图片

->

图片

Summary

图片

Lecture 20: Generative Models II

VAE

图片

图片

图片

Generate

图片

Edit

图片

VQ-VAE

图片

GAN

Structure

图片

Loss

图片

Train

图片

图片

Math

图片

图片

图片

图片

图片